Recursion:
Recursion is a problem-solving technique where the solution of a problem depends on solutions to smaller instances of the same problem. It is a process by which a function calls itself directly or indirectly. Such a function is called a recursive function.
Use of Recursion in” Tower of Hanoi” Problem:
Let’s first understand the “Tower of Hanoi” problem.
- There are 3 pegs A, B, and C.
- n disks of different diameters are placed on peg A so that a larger disk is always below a smaller disk.
- The aim is to move n disks to peg C using peg B as an auxiliary.
- Only the top disk on any peg may be moved to any other peg, and a larger disk may never rest on a smaller one.
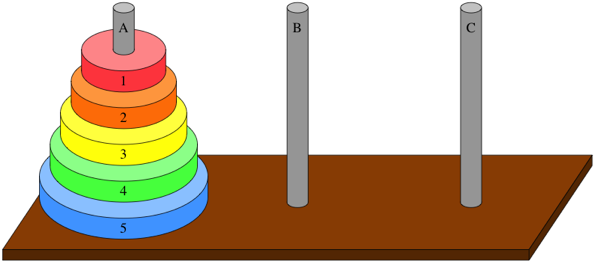
Recursion is a natural choice for solving the Tower of Hanoi problem because of its recursive nature. Here’s how recursion is used:
- For the best case, that is when there is only one disk to move, we can simply move the disk from peg A to peg B.
- When n>1, we can break the problem into smaller subproblems. The general recursive algorithm is:
- Move the top n-1 disks from A to B, using C as an auxiliary.
- Move the remaining disk from A to C.
- Move the n-1 disks from B to C, using A as an auxiliary.
These steps are repeated recursively until a base case is reached.